The investigation of the child’s conception of space conducted by the Swiss psychologist and epistemologist Jean Piaget (1896–1980) in the early 1940s can be read not only as a major contribution to developmental psychology, but also as an ambitious attempt to find a new foundation for geometric intuition. In the late nineteenth and early twentieth centuries, Euclidean geometry’s legitimacy as an exclusively valid description of physical space had been fundamentally relativized, whereby geometric argumentation had lost its status as the royal road of mathematics. It was in this context that Piaget was working on establishing a psychological foundation of geometry. His influential books on the development of the child’s conception of space and geometry, first published together with Bärbel Inhelder and Alina Szeminska in French in 1948, were part of the much larger project of genetic epistemology, which aimed at the investigation of all perceptive and cognitive functions underlying scientific practice (at least in the Western tradition). What kind or style of experimental approach made this project possible? Under which theoretical and instrumental constellations could primordial elements of spatial conception—something by definition hidden from the sight and experience of the adult scientist—be made visible?
In the course of physical and cognitive development, the sensory apparatus adopts a geometric interpretation of the world that will make possible the application of Euclidean notions such as distance, linearity and parallelism. In order to visualize the adaptations that the child must accomplish while learning to see in a correct ‘Euclidean’ manner, Piaget designed various experimental setups. These setups confronted the infants with exercises in applied geometry: the young subjects had to recognize geometric figures and identify them by name; they were asked to tie various knots; at a later stage of development, they had to build perspectives which a doll would perceive from a certain position. And yet much of Piaget’s analysis, particularly his interpretation of the primordial conception of space, relied on a simple paper tool that had been in use in experiments on the child’s perception since 1900: namely children’s drawings.
In one of these experiments, Piaget’s team of psychologists showed geometric figures to the children and asked them to copy the forms with pencil and paper (Fig. 2-3). As early as age three, children were capable of making scribbles that could be differentiated as open or closed forms, but it took another half year or year for the gesture to become controlled and intentional. In many drawings from this stage, the circle (Fig. 2, model 4) was already represented as a closed curve, although the square and the triangle (Fig. 2, model 5 and 6) also resembled closed curves, sometimes with a kind of symbolic indication, such as wavy lines jutting out to indicate angles (as in the copy after model 5). Although incapable of distinguishing between straight and curved figures, the children were already capable of copying the relationships of models 1 to 3 quite convincingly. At this stage a mode of spatial representation that neglects projective and Euclidean relationships altogether (proportions, distances, perspectives with projections and sections) emerges; it arranges the space according to the elementary relations of “proximity,” “separation,” “relationship of order” and “relationships of surrounding or enclosure” as well as “continuity” or “discontinuity.” According to Piaget, these elementary spatial representations “are none other than those relations which the geometricians tell us are of a primitive character, forming that part of geometry called Topology, foreign to notions of rigid shapes, distances, and angles, or to mensuration and projective relations” (Jean Piaget & Bärbel Inhelder: The Child’s Conception of Space, London 1956, pp. 8-9).
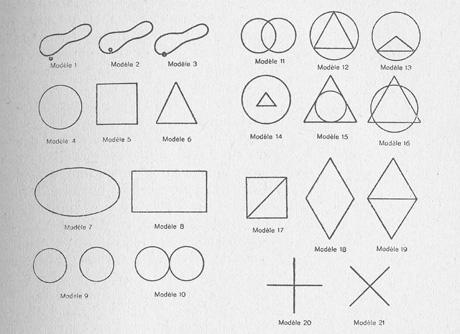
Fig. 2a: Figures for children to copy from Piaget’s experiment on drawing geometric figures as reproduced in: Jean Piaget & Bärbel Inhelder: La représentation de l’espace chez l’enfant, Paris 1948.
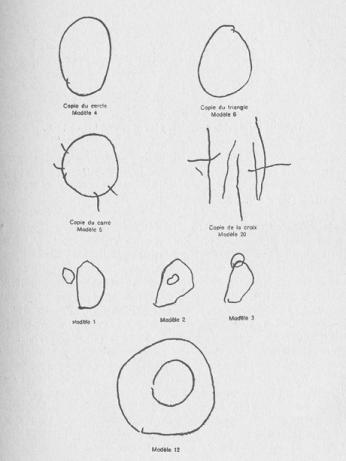
Fig. 2b: Sample drawings from substage IB from Piaget’s experiment on drawing geometric figures (as reproduced in the publication), from: Jean Piaget & Bärbel Inhelder: La représentation de l’espace chez l’enfant, Paris 1948.
Topology—in the proper sense of the term—is a thoroughly modern discipline of mathematics having no ancient roots, which like probability theory emerged during the eighteenth and nineteenth centuries. It developed under the headings Analysis Situs or Geometria Situs around certain problems of orientation or position in space. Since the second half of the nineteenth century, and especially since Bernhard Riemanns and Henri Poincaré’s contributions to the Analysis Situs, this branch of research has been known as topology, and it has become a fundamental field of modern mathematics. Topology deals with properties that remain unaffected when one subjects shapes or spaces to continuous deformation. Objects or figures might be topologically equivalent (homeomorphic) even though they differ in fundamental geometric properties such as length, area, volume, angle or curvature. Topology describes the equivalence between homeomorphic shapes like circles and squares, thereby formalizing orientation itself and constructing objects like knots, incongruent counterparts, or genuinely topological inventions like the Möbius band, that is shapes that cannot be oriented, because the differentiation between left and right cannot be applied to them.
Piaget discovered highly abstract mathematical structures in the child’s primordial conception of space, in the process of which he remained quite aware of the difference between exact operation and intuitive spatial representation (Anschauung). He presupposes that the further development of geometric space should not be understood as the mere realization of physiological functions, but as a product of the child’s interaction with the world, which builds up certain structures of perception and reorganizes spatial conception again and again. Earlier perceptions are continuously revised, not being simply rejected when the child learns more about the world, but remaining effective in a thoroughly transformed way. According to Piaget, the topological drawings of his experimental subjects should be considered traces of surviving sensory experiences that refer back to the formation of sensori-motor perception in the first two years of the infant’s life. Therefore he emphasizes that children’s drawings should not be regarded as immediate inscriptions of spatial perceptions. Instead he considers them to be agents reconstructing structures of spatial perception that have already been developing since the sensori-motor phase. In the child’s belated rational investigation of his own prior perceptions, he follows the chronology of his experiences ab initio, thereby achieving the construction of spatial concepts from an intuitive reflection on his most elementary sensations.
According to Piaget, the origin of spatial representation coincides with the origin of drawing, language and representational thinking in general. In spite of their common development, drawing soon falls behind the mental conception of space (especially in the case of complex and three-dimensional constructions). Yet, in its simplest and earliest appearances, drawing should be conceived as the representation or even the motor of spatial conception, because—here Piaget quotes his teacher, the philosopher of mathematics Léon Brunschvicg—drawing is not founded on geometry, but on the contrary, geometry is founded on the practice of drawing. If one explains the origins of geometry as arising from drawing, the child’s drawing can indeed be operationalized as a reconstruction apparatus of the psychogenesis of space. If one understands drawing in this way, it does not record an independent process of development, rather it documents and reflects its own developmental conditions—and thereby furthers mental ontogeny. Children’s drawings are able to visualize geometric conceptions because they are one of its main motors. The drawing child constitutes a veritable machine that works on the production of a Euclidean future, because—as Piaget detected in his experiments—it helps to complete and partly to conceal the infant’s older tacit topological knowledge.
According to the genetic epistemologist, Euclid’s elements and the topological properties of shapes have their origin neither in the world nor in the history of sciences, but in cognitive schemes that every man and woman builds up in reflexive interaction with objects. Strictly speaking, the child’s perception is not oriented by mathematical structures, on the contrary: every child produces these structures again and again. Through its localization in sensori-motor and cognitive functions, geometry regained a historical timelessness and ideality that it had lost in modern mathematics and physics. And it is exactly this deduction that raises a historical and logical problem: Piaget considers the structures of topology, which were developed 2000 years after Euclid, to be the origin of the ontogenesis of spatial thinking. To put it differently: According to Piaget, children have always had an implicit knowledge of what modern mathematicians could not conceptualize before the introduction of topology around 1900. Piaget’s theory formulates a peculiarly inverted version of Ernst Haeckel’s biogenetic law that unites historical phylogeny and mental ontogeny in a recursive Möbius-band-like figure. Before and after Piaget, children draw towards a Euclidean future—with the decisive difference that after Piaget they will always have already founded the logical principles on which Euclid’s axioms rest.

Fig. 3: Copies of various geometric models (compare Fig. 2a) and stickman made by a four-year-old boy (Jacques), from Piaget’s experiment on drawing geometric figures, 1945. Jean Piaget Archives, Geneva.
This study on Piaget is part of a book project on the history of children’s drawings as research objects and instruments in the human sciences and humanities between 1880 and 1950 (working title: Meaningful Scribbles: An Epistemic History of Children’s Drawings). The project investigates in particular the emergence of children’s drawings as diagnostic, therapeutic and experimental tools, thereby focusing on the different methods, techniques and tests that were developed to ‘read’ that which had previously been thought meaningless. The project is being realized in the context of the research group Knowledge in the Making: Drawing and Writing as Research Techniques, which inquires into the role of graphic inscription techniques in the production of knowledge.
